As professionals in the field of architecture, we understand that the intricate balance between functionality and aesthetics is key to creating exceptional design houses that stand the test of time. One might not immediately associate mathematics with the creative process of designing architectural marvels, but the seamless integration and differentiation of mathematical principles play a crucial role in shaping the spaces we inhabit. Let's delve into how architects harness the power of mathematics to craft the best design houses that leave a lasting impact.
Understanding the Foundation: Integration of Mathematics in Architectural Design
Mathematics serves as the bedrock upon which architectural design principles are built. The concept of integration, both literal and figurative, is fundamental in translating architectural visions into tangible structures. From conceptualizing spatial layouts to analyzing structural stability, architects rely heavily on mathematical concepts to bring their designs to life.
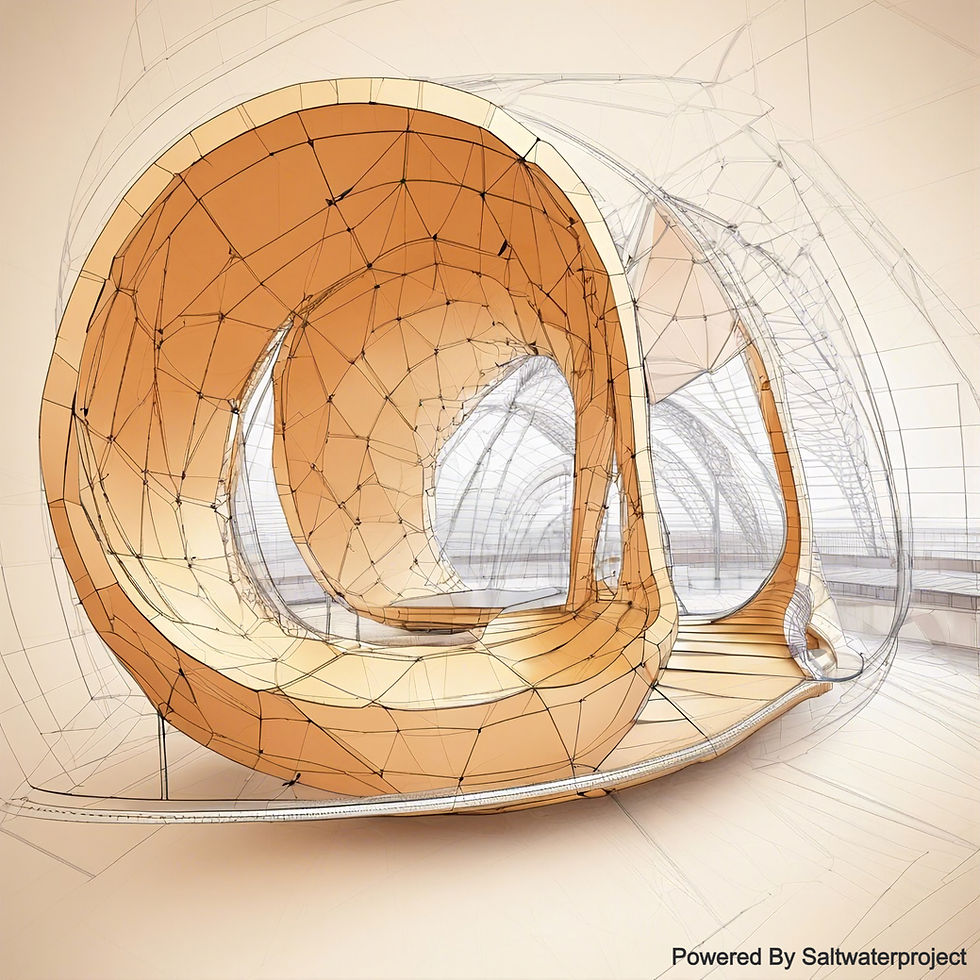
In the realm of architectural design, calculus plays a pivotal role in optimizing spatial layouts. By utilizing mathematical techniques such as differentiation, architects can determine the optimal distribution of space within a structure. This not only enhances the functionality of the design house but also ensures that every square foot is utilized efficiently. When it comes to constructing Building that are not only aesthetically pleasing but also structurally sound, Structural Engineers turn to mathematics to perform detailed structural analyses. Through the integration of mathematical formulas and principles, architects can calculate load-bearing capacities, stress distributions, and other critical factors that dictate the structural integrity of a building.
Embracing Complexity: Differentiation in Architectural Design
Differentiation in mathematics involves the process of finding the rate at which quantities change. In architectural design, this concept is applied to create dynamic spaces that not only serve their intended purpose but also captivate the senses. Let's explore how architects leverage differentiation to infuse complexity and innovation into their designs.

By differentiating mathematical equations, architects can introduce curves and organic forms into their designs. This approach adds a layer of sophistication and fluidity to designing houses, breaking away from traditional geometric constraints and fostering creativity in architectural expression.
`Advancements in computational design tools have revolutionized the way architects approach differentiation in architectural design. Through the use of parametric design software, architects can manipulate complex mathematical algorithms to generate intricate patterns, shapes, and structures that push the boundaries of traditional design aesthetics.
Harmony Between Integration and Differentiation: A Symphony of Mathematics in Architectural Design
The true beauty of architectural design lies in the harmonious interplay between the integration and differentiation of mathematical principles. When architects strike the perfect balance between these two facets, they can create buildings that not only exude architectural brilliance but also provide a harmonious living experience for occupants.
The Guggenheim Museum in Bilbao, Spain stands as a testament to the harmonious fusion of art and mathematics. Architect Frank Gehry's visionary approach to design is exemplified in the fluid curves and intricate geometries that define this iconic structure. Through a meticulous application of mathematical principles like calculus and differentiation, Gehry was able to achieve a level of architectural sophistication that transcends conventional boundaries. The seamless integration of mathematical precision with artistic creativity allowed Gehry to push the boundaries of what was thought possible in architectural design. Each curve and angle in the Guggenheim Museum serves a purpose beyond mere aesthetics, reflecting a deep understanding of mathematical concepts that underpin the structure's form and function. Visitors to the Guggenheim Museum are not only treated to a visually stunning experience but also an intellectual journey through the intricate interplay of mathematics and art. Gehry's innovative use of mathematical principles has not only redefined the architectural landscape but has also inspired a new generation of designers to explore the boundless possibilities that arise from the convergence of science and creativity.
Conclusion: Elevating Architectural Excellence through Mathematics
In the realm of architectural design, mathematics serves as the silent partner that elevates creativity to new heights. By embracing the principles of integration and differentiation, architects can transcend conventional boundaries and craft design houses that not only inspire awe but also stand as testaments to the profound impact of mathematics on the built environment. As professionals in the field of architecture, let us continue to explore the boundless possibilities that arise from the fusion of mathematics and design. By harnessing the power of mathematics, we can unlock the potential to create design houses that are not just structures but living works of art that resonate with the essence of architectural excellence.
So, the next time you embark on a new architectural project, remember the profound influence of mathematics and how the integration and differentiation of its principles can guide you towards designing the best design that leaves a lasting legacy in the world of architecture.
By embracing the principles of integration and differentiation, architects can transcend conventional boundaries and craft design houses that not only inspire awe but also stand as testaments to the profound impact of mathematics on the built environment.
Let mathematics be your compass, and architectural design be your canvas.
Thank you for reading.
What you think? Is Mathematics necessary in Architectural Design?
Yes
No
Comments